Speak Only About What You Have Read: Can LLMs Generalize Beyond Their Pretraining Data?

Unveiling the Limits and Wonders of In-Context Learning in Large Language Models

In-context learning is one of the secret weapons that has made Large Language Models so successful, but even today, many points remain unclear. What are the limits of this incredible capability? Where does it come from? Is it the secret ingredient to allows LLMs to bring us closer to artificial general intelligence?

In-context learning: the secret skill of a LLM

One of the most amazing capabilities of Large language models (LLMs) is in-context learning (ICL). By simply providing a few examples to a model, it is able to generate a response, mapping input to output. For example, by providing some examples of translation between two languages, the model understands that it must conduct a translation.

We could generalize this concept as the fact that the model succeeds in mapping a function between two elements. Or that, for example ‘house = function(maison)’, so the model must be the examples to understand this function that transforms the input ‘maison’ to ‘house’.

This behavior is not restricted only to language but also to other tasks. For example, Garg showed that a transformer can learn through in-context learning linear functions. In this work, they showed that a Transformer can also learn complex functions (high-dimensional and non-linear) from in-context examples. Surprisingly, Transformers can outperform dedicated models designed for these tasks.

Despite being one of the most interesting skills in LLMs, there are still unclear points about its origin. For example, what is the effect of the pretraining dataset?

Considering the huge amount of data used to train LLMs, it is difficult to answer this question. In several studies, ICL has been achieved even by training a model with a small dataset. For example, Garg trained the model from scratch, using a set of inputs and labels that can be defined as follows:

((x1, f(x1)),(x2, f(x2)), . . .(xn, f(xn)))

As can be seen, we are providing the model with an input x and the result of a function f applied to input x. Once trained the model is asked to predict the result of f(xn+1) for an input xn+1.

In few-shot learning, we ask a model to predict f(xn+1) given a small set of examples, which can be represented as:

(x1, f(x1), x2, f(x2), . . . , xn, f(xn+1))

Previous work (such as this and this) has shown that a transformer can learn many types of data distributions for (x, f(x)). All this simply by showing examples obtained with different functions and different classes of functions.

In general, the model succeeds in learning different classes of functions, but what if the examples in few-shot learning are out-of-distribution? Or of function classes not seen during training?

Can a transformer generalize out of distribution?

What is the relationship between the composition of the pretraining data-set and few-shot learning skills?

Google researchers have been asking themselves the same question and recently published a paper about it:

The transformer is a model that is trained with a simple objective: given a sequence of tokens, the model must predict the next token.

These tokens need not be words. Garg, in previous work, took covariates from a normal distribution and then transformed them with a function f from a class of functions. Using this system as pertaining, the model during in-context learning manages to learn unseen functions derived from the same class of functions.

An example, if the model is trained on linear function classes, the model is capable of performing like a traditional machine learning model. Simply put, given the various examples in the prompt it is capable of modeling the function that maps them. The same is true if it is trained with data generated from decision trees, ReLU networks, and so on.

Garg et al. argues transformers generalize well to tasks/function drawn from the same distribution as the training data. However, one general open question is how these models perform on examples that are out-of-distribution from the training data. (source)

So the next step is to train the model on a set of feature classes and then test what happens when there is data derived from other classes in the ICL prompt.

The authors at Google did exactly that they chose a decoder model (9.5 M parameters, 12 layers, 8 attention heads like Garg) and tested it on different classes of D(F) functions: linear functions, sparse linear functions, two-layer ReLU networks, and sinusoidal functions. In addition, the authors used data mixtures generated by combining multiple distinct families of functions. For example, considering a class of functions D(Fa) one can create a mixture with D(Fb) simply:

D(F) = w · D(Fa)+ (1−w)· D(Fb)

This approach is interesting because it allows us to investigate how the model selects among various function classes when presented with examples of in-context learning.

we find that the models make optimal (or nearly so) predictions after seeing in-context examples from a function class which is a member of the pretraining data mixture (source)

The authors note that a model that is trained with a mixture of function classes performs well in ICL as models pre-trained on only one function class.

Another interesting result is that the ICL is uniform for the number of examples that are given. Moreover, even varying the mixture of functions the model performs as well as if it were trained on the pure class function (e.g., if trained on a mixture of dense and sparse functions it shows iCL on sparse functions as a model trained only on sparse functions)

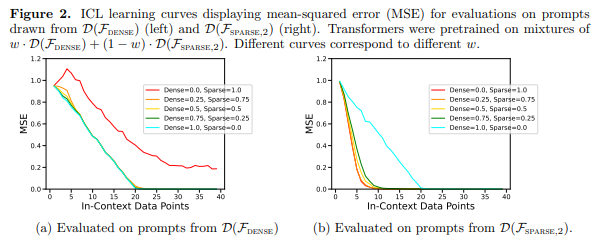
While these were expected results, the authors note something interesting:

Figure 2 also demonstrates that transformer model ICL generalization suffers outof-distribution. Even though dense and sparse linear classes are both linear functions, we can see the poor performance of the red curve in Figure 2a (which corresponds to a transformer pretrained on only sparse linear functions and evaluated on dense linear data) and vice-versa for the teal curve in Figure 2b (source)

In other words, the model is unable to generalize if it has not seen that class of functions during pretraining.

The authors decided to go deeper into this behavior. So, they decided to test the behavior of the model in two cases:

• ICL performance for feature classes that the model could plausibly predict even though it did not see during training. For example, convex combinations of functions drawn from the pretraining function classes.
• ICL performance on functions which are extreme versions of functions seen in pretraining. For example, if the model saw sinusoidal functions in the pretraining in a few shots, it sees functions at much higher or lower frequency).

The results are not exciting. If the function is close enough to that seen during pretraining, the model approximates it well. If not, no, the predictions are erratic.

The authors question whether this stems from the model.

Figure 3a shows that the transformer’s predictions at moderate sparsity levels (nnz = 3 to 7) are not similar to any of the predictions from either of the function classes provided at pretraining, but rather, something in between the two (source)

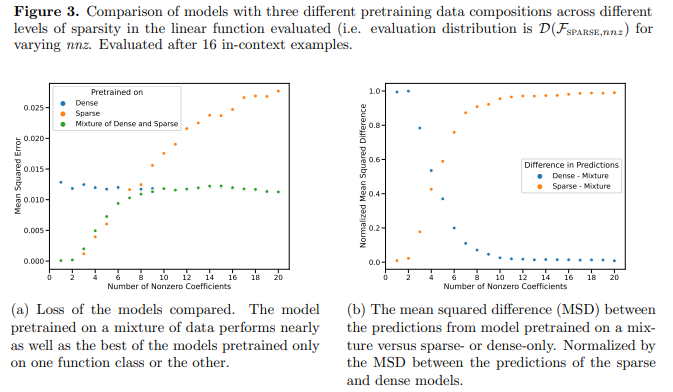
They hypothesize that the model has an inductive bias that allows it to combine pre-trained function classes in nontrivial ways. That is, the model can produce predictions by combining the functions it saw during training. To test this, the authors decide to use disjointed functions (“perform ICL on linear functions, sinusoids, and convex combinations of the two”).

The model is trained with a combination of linear and complex functions:

D(F) = 0.5·D(Fdense)+0.5·D(Fsine))

is able to predict correctly for these functions separately but fails to fit a function for a convex combination of the two.

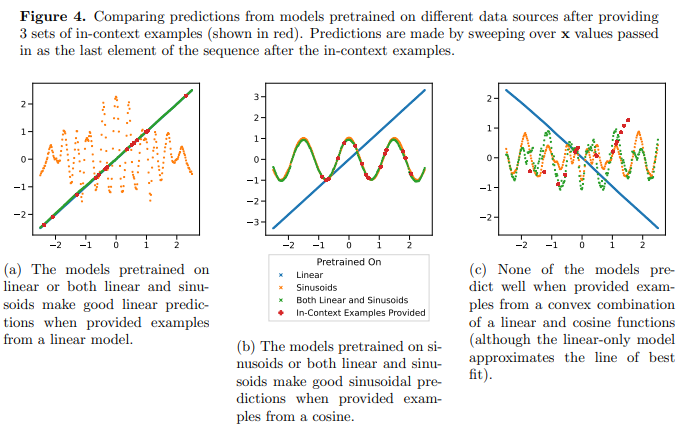
This suggests that the interpolation phenomenon shown in Figure 3b for linear functions is not a generalizable inductive bias for in-context learning in transformers. However, it continues to support the narrower hypothesis that when the in-context examples are close to a function class learned in pretraining, the model is capable of selecting the best function class to use for predictions. (source)

The authors, however, note that when the combined function is predominantly from one function class (or the other), the model succeeds in approximating well. In contrast, it fails when both functions contribute to the mixture. This confirms that the model’s predictions are limited to pretraining.

Parting thoughts

The authors studied the role of pretraining data composition for the performance of the LCI, both in the context that feature classes are inside and out of the pretraining data distribution.

We found that the pretrained transformers struggle to predict on convex combinations of functions drawn from pre-training function classes, and (2) We observed that transformers can generalize effectively on rarer sections of the function-class space and still break down as the tasks become out-of-distribution. (source)

Translated, the transformer is unable to generalize for functions that are outside the distribution he saw during pretraining.

The first question is: how to apply these results to large language models?

Actually, it is not easy to be able to test the same thing empirically with LLMs. First, because LLMs are trained on a huge corpus. Second, translating these kinds of experiments is not easy.

In summary, these results indicate:

• The transformer cannot generalize beyond what he saw during pretraining.
• ICL is highly dependent on what is in the pretraining and therefore, more broad pretraining data must be provided to increase ICL capabilities.

What do you think? Let me know in the comments

If you have found this interesting:

You can look for my other articles, and you can also connect or reach me on LinkedIn. Check this repository containing weekly updated ML & AI news.

Here is the link to my GitHub repository, where I am collecting code and many resources related to machine learning, artificial intelligence, and more.

or you may be interested in one of my recent articles:

Reference

Here is the list of the principal references I consulted to write this article (only the first author name of an article is cited).

1. Yadlowsky, 2023, Pretraining Data Mixtures Enable Narrow Model Selection Capabilities in Transformer Models, link
2. Garg, 2022, What Can Transformers Learn In-Context? A Case Study of Simple Function Classes, link
3. Li, 2023, Transformers as Algorithms: Generalization and Stability in In-context Learning, link
4. Akyurek, 2022, What learning algorithm is in-context learning? Investigations with linear models, link