Mathematics Challenge

Oxford University Calculus Challenge

2023 Oxford Mathematics Admission Test

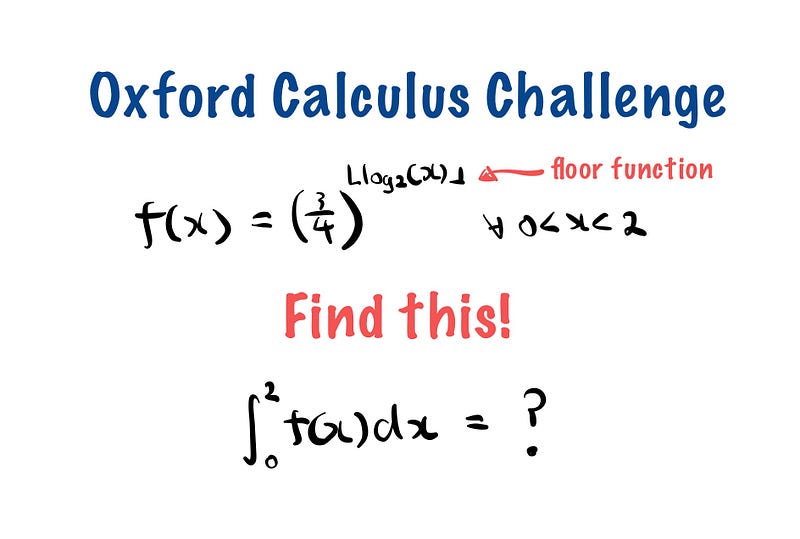
We looked at a geometry problem on the Oxford Mathematics Admission Test yesterday. If you think you have a chance to get into Oxford University, take a look at today’s problem.

Here’s a hint: while solving the challenge, you should be able to find a geometric sum …

I recommend you to pause the article, grab your pen and paper, and give this a go. When you are ready, keep reading for the solution! ✒️

Solution

The tricky part about this question is the nature of the floor function applied to a logarithm.

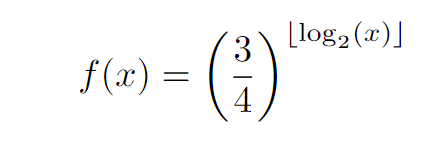
The floor function, as stated, takes the largest whole number that is less than or equal to x. For example ⌊3.6⌋ = 3 and ⌊-1.5⌋ = -2.

What happens when we apply the floor function to a logarithm of base 2? In fact, we are interested in its behavior for 0 < x < 2.

I have picked out some values of x to plug into the function. When x = 2, the resulting output is 1 and when x = 1, the result output is 0. What about values in between 2 and 1? Say 3/2?

In fact this is equivalent to asking

Knowledge of logarithms tells us x must be less than 1 and greater than 0.

This means ⌊log2(3/2)⌋ must be 0. And this holds true for all values 1 ≤ x < 2.

What about when x = 1, x = 1/2, x = 1/4 and so on?

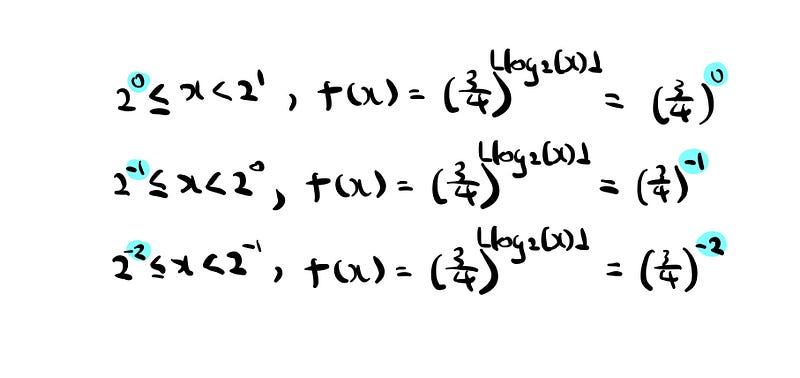
We partition the whole interval [0, 2] into infinitely many sections where the length of each section is from 2^n to 2^(n+1). The biggest section is when n = 0 such that we have 2⁰ = 1 and 2¹ = 2.

If we pay close attention now, we see that for the interval starting with 2^n, the output from the floor function of logarithm with base 2 results in n.

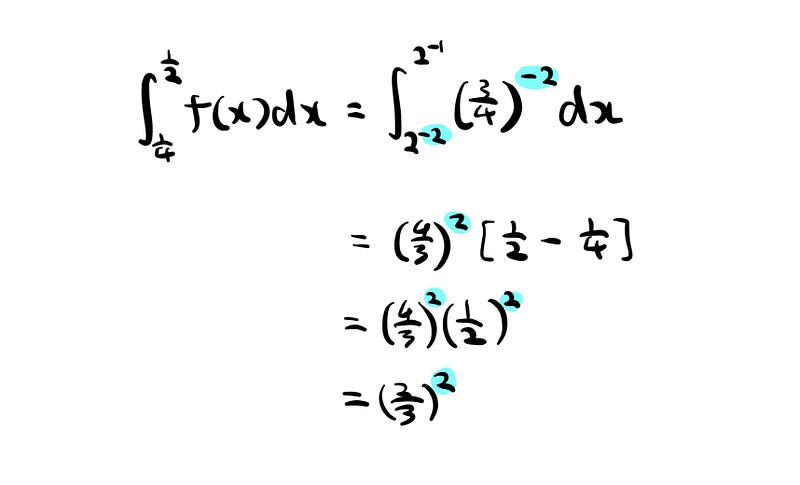
I have given an example above. The integral considers the function from 1/4 to 1/2, or 2^(-2) to 2^(-1).

Here’s a task for you. Try and find the integral when x ranges from 1/8 to 1/4. What about from 1/16 to 1/8? And so on?

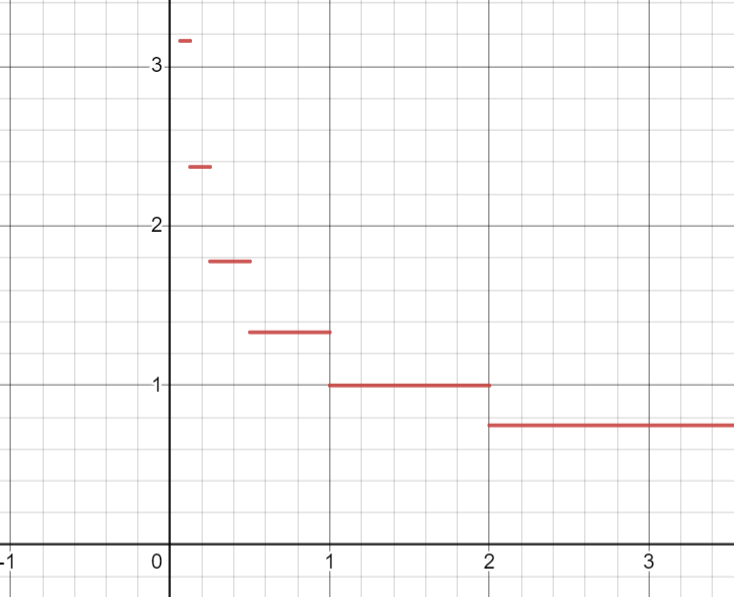
Recall the aim of the question, which is to evaluate the integral of the function from 0 to 2.

Now the integral is equal to the sum of infinitely many integrals with 2^n to 2^(n+1) each for each segment, or geometrically, the total area of infinitely many rectangles.

Let’s write out the whole sum.

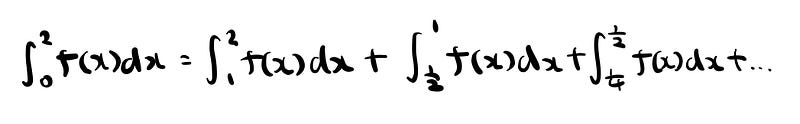
It goes all the way to infinity, where the bounds become arbitrary close to 0 and 1/2^n.

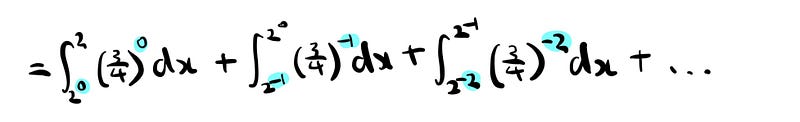
Now from the set up above, we should see this pattern for every integral, and in fact, upon computing the first few, we see the following geometric series!

Convince yourself that the highlighted terms are equivalent.

This pattern continues ad infinitum and so the common ratio is in fact 2/3.

Finally, the geometric sum is convergent.

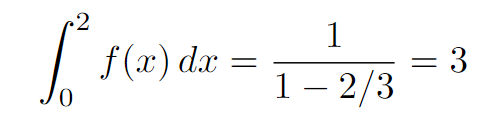
The answer is c.

Thank you for reading. Don’t forget to clap the article if you find it insightful.

You can also support me with ko-fi ☕.