Leave-One-Out Cross-Validation (LOO-CV): An Essential Tool for Model Validation and Selection

Introduction

In the realm of statistical modeling and machine learning, validating the predictive power of a model is as crucial as its construction. Leave-One-Out Cross-Validation (LOO-CV) stands as a pivotal technique in this validation process, offering a rigorous method for assessing the performance of statistical models. This essay delves into the concept, methodology, advantages, and limitations of LOO-CV, underscoring its significance in the field of data science.

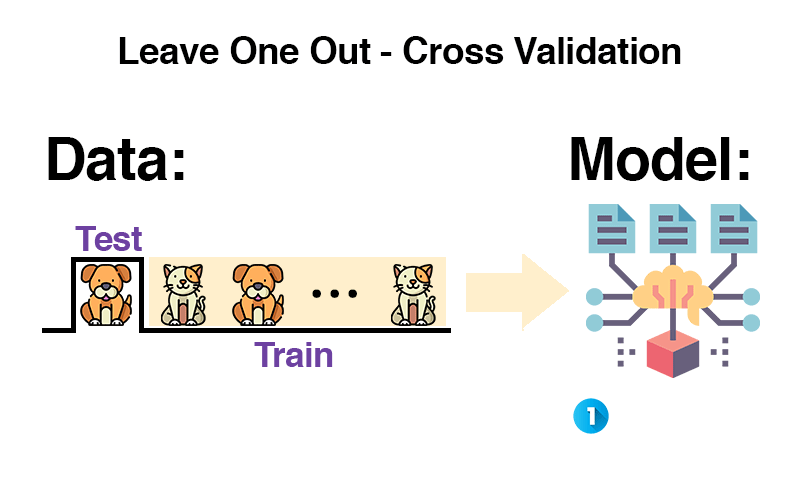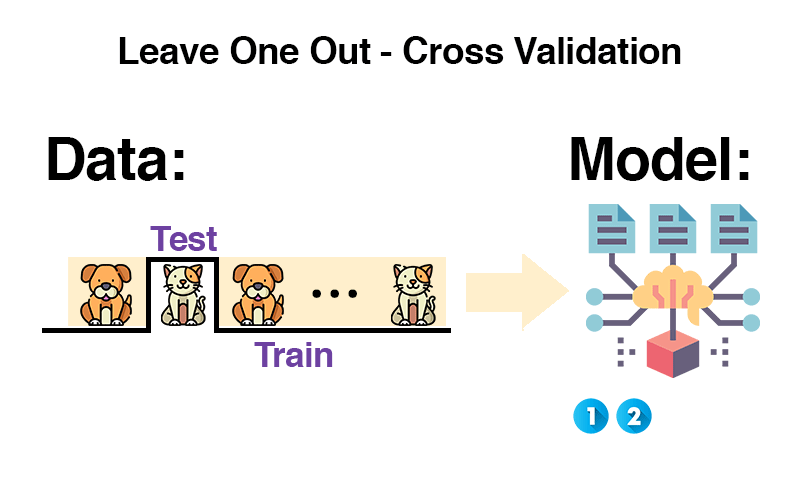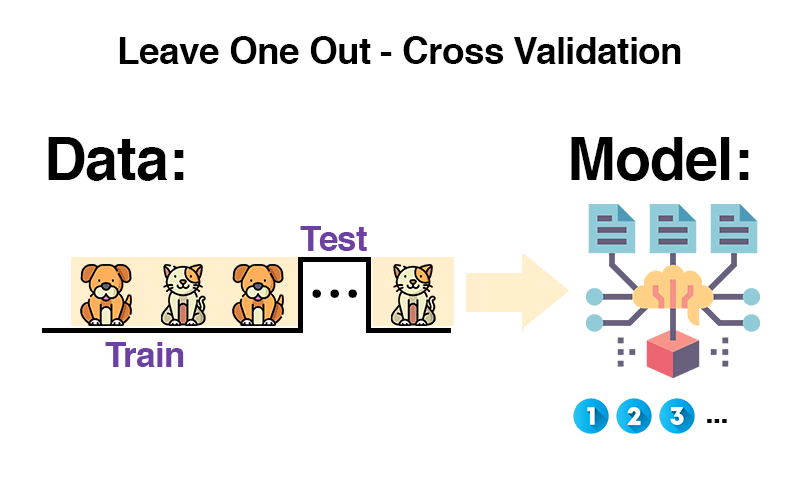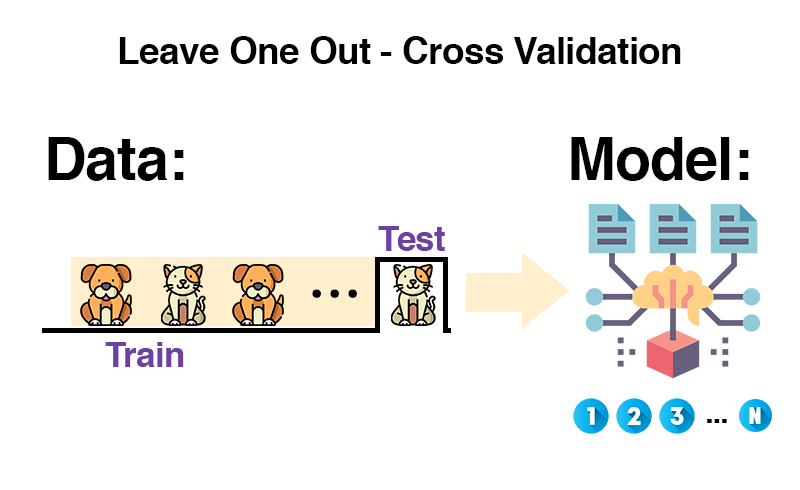
Leave-One-Out Cross-Validation: A single step of separation for a leap in understanding, ensuring every point tells its story and every model listens closely.

Concept and Methodology

LOO-CV is a model validation technique used to evaluate the predictive performance of statistical models. It falls under the umbrella of cross-validation methods, which are designed to assess how the results of a statistical analysis will generalize to an independent data set. The unique aspect of LOO-CV is its approach of using a single observation from the original sample as the validation data, and the remaining observations as the training data.

The process involves iterating through each data point in the dataset. In each iteration, the model is trained on all data points except one, and the model’s prediction is tested on the left-out data point. This cycle repeats for each data point in the dataset, thus the name ‘Leave-One-Out’.

Advantages of LOO-CV

1. Reduced Bias: By using nearly, the entire dataset for training, LOO-CV minimizes the bias that can occur in other cross-validation methods where the training set is substantially smaller than the original dataset.
2. Model Robustness: It provides a comprehensive assessment of how the model performs across different subsets of data, highlighting its robustness or lack thereof.
3. Useful for Small Datasets: LOO-CV is particularly beneficial for small datasets where preserving the maximum amount of training data is crucial.

Limitations and Considerations

1. Computational Intensity: For large datasets, LOO-CV can be computationally expensive as it requires fitting the model as many times as there are data points.
2. Variance in Estimates: This method can lead to higher variance in the testing phase because it repeatedly evaluates the model on very similar datasets.
3. Outlier Sensitivity: LOO-CV may be overly sensitive to outliers since each model iteration is tested on a single data point.

Applications

LOO-CV finds its applications in various fields, from machine learning and artificial intelligence to econometrics and bioinformatics. It is instrumental in fine-tuning models, selecting appropriate model parameters, and ultimately in the decision-making process regarding the best model to deploy for prediction tasks.

Code

To demonstrate Leave-One-Out Cross-Validation (LOO-CV) in Python, we can use a synthetic dataset and a simple regression model as an example. We will also plot the results to visualize the performance of the model across different iterations of LOO-CV. For this demonstration, we will use libraries such as numpy for data manipulation, matplotlib for plotting, and sklearn for the regression model and LOO-CV.

First, let’s create a synthetic dataset. We will generate a simple linear relationship with some added noise. Then, we’ll use a linear regression model and apply LOO-CV to this dataset. Finally, we’ll plot the predicted vs actual values for each iteration of the LOO-CV.

Let’s proceed with the code.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import LeaveOneOut
from sklearn.metrics import mean_squared_error

# Creating a synthetic dataset
np.random.seed(0)
X = np.random.rand(100, 1) * 10  # 100 data points
y = 3 * X.squeeze() + np.random.randn(100) * 2  # Linear relation with noise

# Initialize linear regression and LOO-CV
model = LinearRegression()
loo = LeaveOneOut()

# Arrays to store actual and predicted values for plotting
y_real = []
y_predicted = []

# Applying LOO-CV
for train_index, test_index in loo.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

    model.fit(X_train, y_train)
    y_pred = model.predict(X_test)

    y_real.append(y_test[0])
    y_predicted.append(y_pred[0])

# Plotting
plt.figure(figsize=(10, 6))
plt.scatter(y_real, y_predicted, alpha=0.7)
plt.plot([min(y_real), max(y_real)], [min(y_real), max(y_real)], color='red')  # Line for perfect predictions
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('LOO-CV: Actual vs Predicted Values')
plt.grid(True)
plt.show()

The plot above visualizes the results of the Leave-One-Out Cross-Validation (LOO-CV) applied to our synthetic dataset using a linear regression model. In this plot:

• Each point represents a single iteration of the LOO-CV process.
• The x-axis shows the actual values of the left-out data point in each iteration.
• The y-axis displays the predicted values by the model trained on the remaining data.

The red line represents the line of perfect prediction, where the predicted values exactly match the actual values. The closer the points are to this line, the better the model’s predictions for that iteration of LOO-CV.

This visual representation offers an insight into how well the model is performing for each individual data point when trained on the rest of the dataset. It’s a powerful tool for understanding model behavior and diagnosing potential issues like overfitting or underfitting, especially in small datasets or datasets with high variability.

Conclusion

Leave-One-Out Cross-Validation is a powerful tool in the model validation arsenal. Its capacity to thoroughly assess a model’s predictive ability, especially in scenarios with limited data, makes it invaluable. However, its practical application requires a balance between computational feasibility and the need for precise model evaluation. Understanding its advantages and limitations is key to leveraging LOO-CV effectively in statistical modeling and machine learning endeavors.